TMS Analytics & Physics library is a set of classes that provide functionality for building powerful math applications with Delphi. In the new version 3.2 of the library, we introduced special FNC math components. The components bring new possibilities to develop and tune your math application in design-time with standard IDE tools.

In this article, we’ll consider the base concepts of the FNC math components and provide information on how to work with functions, derivatives, and integrals.

All FNC math components are nonvisual. Each component implements some math concept and provides properties to manipulate and tune it in design- and run-time. Let’s consider the following components:

• TFNCProvider – creates math environment; allows introducing variables and parameters for function evaluations, symbolic derivatives, and integrals.
• TFNCFunction1D – introduces a symbolic function of one variable; allows evaluating the function for the specified variable value.
• TFNCDerivative1D – introduces a symbolic derivative of a math expression; allows evaluating the derivative for the specified variable value.
• TFNCIntegral1D – introduces a symbolic integral of a math expression; allows evaluating the integral for the specified variable value.

To begin any FNC math application we first need to put a TFNCProvider component on the form. The component has two published properties:

• Variables (TVariableCollection) – a collection of variables that can be used as arguments of functions.
• Parameters (TParameterCollection) – a collection of parameters that can be used in the math environment to build functions, derivatives, integrals, and other math expressions.

When you put a TFNCProvider on the form in design-time, it automatically creates a default variable ‘x’ for your math application. You can change the name of the variable or add/delete variables at design- and run-time.

For the simplest math application, the default environment with one variable ‘x’ is enough. So, let’s go forward and consider the next FNC component TFNCFunction1D and its properties:

• Provider (TFNCProvider) – a math environment for the function.
• Variable (TVariableProperty) – a variable specifying the argument of the function.
• Formula (TFormulaProperty) – a formula specifying the math expression of the function.

Placing a TFNCFunction1D on the form, it assigns the default value ‘x’ to the Variable property. We need to set up the Provider property and the expression for the Formula property, say ‘5*sin(6*x)’ in the Object Inspector. The resulting properties are shown in the picture below: 

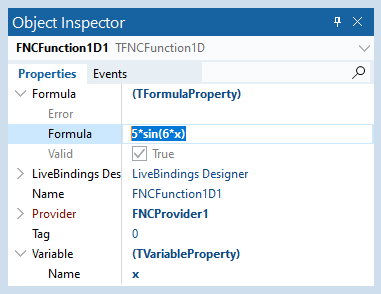
The function is ready to use. What can we do with it? The first idea is to draw the function and see what it looks like. We have the TFNCFunction1DPlotter component especially developed for this purpose:

• TFNCFunction1DPlotter – a binding for an FNC function component and an FNC Chart; allows drawing any FNC function on the chart.

The component has several published properties that we can use to tune it and show a function on the FNC Chart:

• Provider (TFNCProvider) – a math environment for the component.
• Min (TValueProperty) – the minimal value of the variable range to plot the function.
• Max (TValueProperty) – the maximal value of the variable range to plot the function.
• PointCount (Integer) – number of points to plot the function.
• AFunction (TFNCBaseFunction1D) – a FNC function to plot.
• AssignLegend (Boolean) – if true, assigns the function’s expression to the serie’s legend.
• Chart (TTMSFNCChart) – an FNC chart to draw the function.

First, we need to assign the appropriate Provider property. The Min and Max properties have default values ‘0’ and ‘10’ accordingly, and the PointCount is 50.

When you assign the Chart property in design-time, the component automatically creates a new serie for the chart. The function will be drawn with this serie and you can set the appropriate properties of the serie to get the suitable representation of the function.

For now, we have a simple math application, designed with the four components: a provider; an FNC function; an FNC plotter; and an FNC chart. The form in design-time is shown in the picture below:

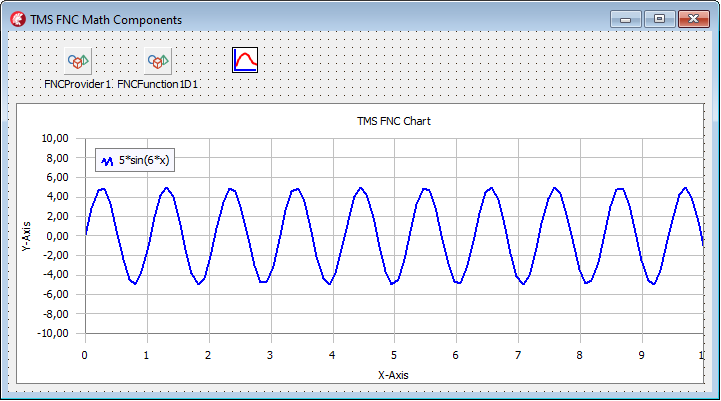
In run-time, the application works like in design-time: it shows the only function ‘5*sin(6*x)’. Let’s move on and get the application drawing any function, the user can input as a math expression.

First, let’s look at the Parameters property on the FNC provider component. This is a collection of parameters. A parameter is a named value that can be used in math expressions together with variables. The TParameterProperty class has the following published properties:

•  Name (String) – name of the parameter.
• Value (String) – constant math expression of the parameter’s value.
• RealValue (Real) – read-only float number for the math expression.

Via common IDE’s interface, we can add or remove items of the Parameters collection to get desired math environment. For our application, we created three new parameters and assigned them some values, as shown in the following picture:

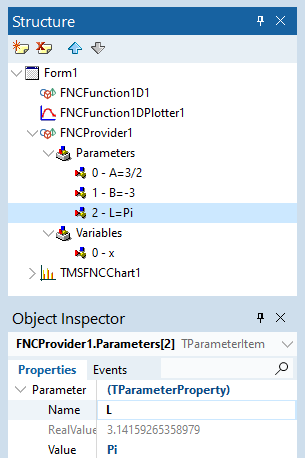
Now we can create a simple user interface to input a math expression in a text box and a button with the following event handler:

procedure
TForm1.Button1Click(Sender: TObject);
var
  f: string;
begin
  f:= Edit1.Text;
 
  FNCFunction1D1.Formula.Formula:= f;
end;
 

Thus, in run-time, the user can draw on the chart any function that depends on the variable ‘x’ and three parameters ‘A’, ‘B’, and ‘L’. Here is an example of one such function draw:

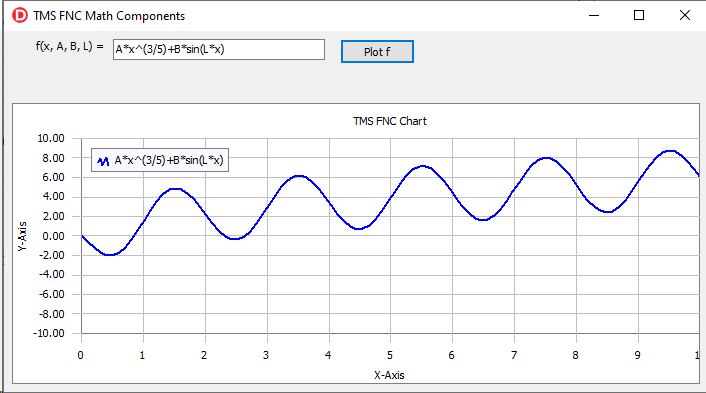
The values of the parameters can be changed as in design-time as in run-time. If a function depends on the parameter, changing the value immediately leads to the function and the chart update.

The TFNCDerivative1D component is intended to work with derivatives and has the following properties:

•  Provider (TFNCProvider) – a math environment for the component.
• Variable (TVariableProperty) – a variable specifying the argument of the function.
•  D (TVariableProperty) – a variable specifying the differential.
• Functional – a differentiable math expression.
• Formula (TFormulaProperty) – read-only formula denoting the resulting math expression of the derivative.

In general, this component works like an FNC function, but it evaluates the derivative of the functional expression. Putting the component on the form we can create another button with a simple event handler to draw derivative of any function:

procedure
TForm1.Button2Click(Sender: TObject);
var
  f: string;
begin
  f:= Edit1.Text;
 
  FNCDerivative1D1.Functional:= f;
  FNCFunction1DPlotter1.AFunction:=
FNCDerivative1D1;
end;

Here we showed the resulting application in run-time for the derivative of a simple math expression:

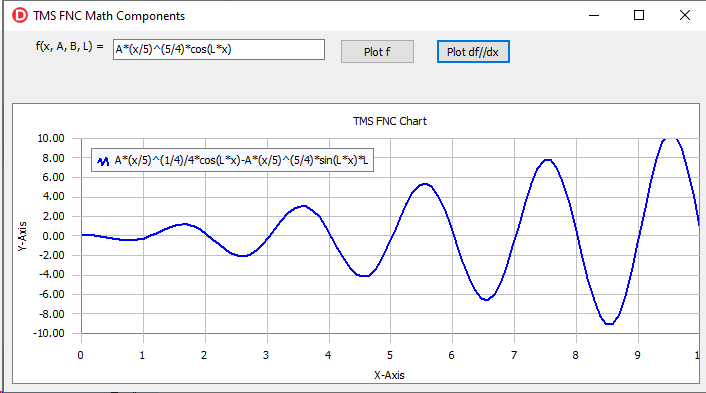
The TFNCIntegral1D component has the same properties as the described TFNCDerivative1D component, but it evaluates the indefinite integral of a math expression. An example of an integral is shown in the picture below:

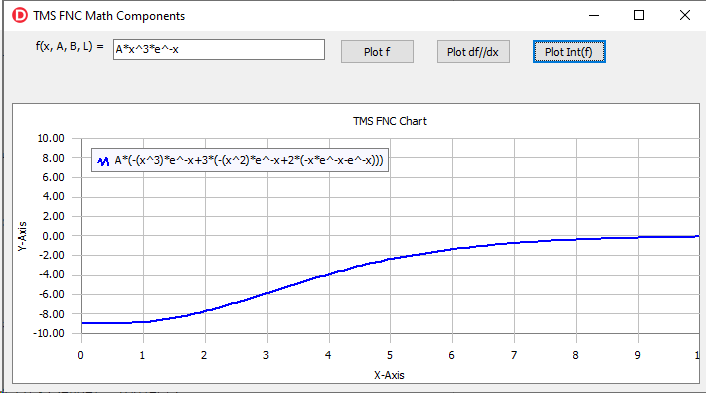
The source code of the demo project for the article can be downloaded from here. To start developing your FNC math application you need the latest versions of TMS Analytics & Physics and TMC FNC Chart products.