Blog
All Blog Posts | Next Post | Previous Post
Implicit integral operator in TMS Analytics & Physics 3.0
Thursday, September 26, 2019
The main new capability of TMS Analytics & Physics 3.0 library is symbolic integration. As the integration realized, the library now allows using ‘implicit’ integral operator in math expressions. Implicit operators allow writing math expressions in short form and manipulate with them without using explicit formula. For example, the expression ‘sin(n*x)+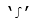
(A*x+B)^2
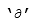x’ contains implicit indefinite integral and the library allows making operations with the expression without using explicit formula of the integral.
Implicit integral operator syntax is the following:
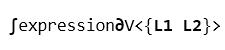
where
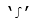is the integral operator; 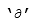is the derivative operator symbol; expression – symbolic expression, integrand of the operation; V – integration variable; L1, L2 – limits of integration. The limits can be omitted, so, the implicit operator can be used for definite and indefinite integrals. There are some examples of syntactically correct expressions with the implicit integral operator:
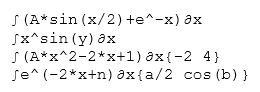
Let us consider an example of how to calculate the value of an expression, containing an implicit integral operator:
The evaluation of the expression containing the indefinite integral implemented with the same method Calculate of the TTranslator class. It allows not using explicit expression of the integration. Internal evaluation system of the library implements the symbolic integration inside the core algorithm. Nevertheless, all required data must be provided for the algorithm to process the expression. Namely, all required variables must be added to the instance of the translator:
- translator.Add('A',-1);
- translator.Add('B', 2);
- translator.Add('n', 3);
- translator.Add('x', 0.5);
Another example is using implicit expression for the definite integral:
One difference between the examples is that the latter does not require the ‘x’ variable value for handling the expression. This is because after using Newton-Leibniz axiom for the definite integral, the expression depends only on ‘A’, ‘B’ and ‘n’ variables. The explicit expression for all implicit operations can be found using the ‘Explicit’ method of the TTranslator class as in the following code:
As the limits of the definite integral are constant and the integrand expression contains only ‘x’ variable the result of the evaluation is constant too, namely ‘392/3’. Nevertheless, it is a symbolic expression, not a floating value. Math expressions with implicit integral operations can be converted into the TeX format to draw as math formulae (https://www.tmssoftware.com/site/blog.asp?post=515). There are some examples of the expressions and drawn formulae:
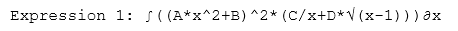
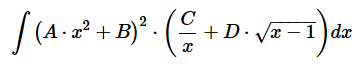
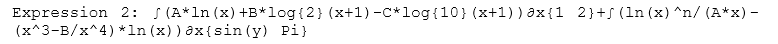
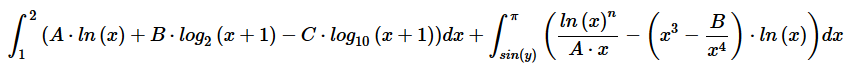
The version 3.0 is already available. Source code of the demo project for the article can be downloaded from here.
Masiha Zemarai
This blog post has received 2 comments.
2. Saturday, September 28, 2019 at 11:33:52 AM
Maybe this is helpful for you for now:https://stackoverflow.com/questions/10137105/delphi-component-or-library-to-display-mathematical-expressions
Bruno Fierens
All Blog Posts | Next Post | Previous Post
van der Linden Scott`