Blog
All Blog Posts | Next Post | Previous Post
Exploring parametric ODE with TMS Analytics and Physics numerical tool
Thursday, July 13, 2017
Ordinary differential equations (ODE) used in many applications for physical, economical and other problem solution. The equations commonly describe the time evolution of some system from known initial state – initial value problem (https://en.wikipedia.org/wiki/Initial_value_problem).The TMS Analytics and Physics pack contains the ODE solution tool of solving initial value problems for systems of ODEs. This tool is totally integrated with the symbolic capabilities of the library. This allows solving parametric problems and exploring how the parameter value influences the system behavior.
Let us consider the following simple parametric ODE:
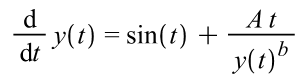
with initial condition y(0)=1 on the time interval t=[0, 10]. The problem is parametric because there are parameters ‘A’ and ‘b’ in the equation. Our goal is exploring how the solution (function y(t)) depends on the value of ‘b’ parameter.
First we create the instance of analytical ODE object, here is the code:
var
A, b: TVariable;
prms: TArray<TVariable>;
fv, equations: TArray<string>;
ode: TAnalyticalODE;
solver: TODESolverClass;
y0: TArray<TFloat>;
t: TArray<TFloat>;
y: TArray<TArray<TFloat>>;
i: Integer;
begin
A:= TRealVariable.Create('A', 1.0); // 1
b:= TRealVariable.Create('b', 0.0); // 2
prms:= TArray<TVariable>.Create(A, b); // 3
fv:= TArray<string>.Create('y'); // 4
equations:= TArray<string>.Create('sin(t)+A*t/y^b'); // 5
ode:= TScalarODE.Create('t', fv, equations, prms); // 6
...
Line 2: Create the variable for ‘b’ parameter.
Line 3: Create array of parameters.
Line 4: Create array of function names (one name required for the problem).
Line 5: Create array of equations (one equation).
Line 6: Create the instance of analytical ODE system with specified equation and parameters.
After the instance of the analytical ODE system created we must select appropriate solver and specify initial condition for the problem. We will use the Runge-Kutta direct solver of the 4-th order. The code continued:
solver:= TRungeKutta4Solver; // 7 y0:= TArray.Create(1.0); // 8
for i:=1 to 8 do begin ode.Parameters['b'].Value:= TValue.From(i); // 9 y:= solver.Solve(ode, y0, 10.0, 1000, t); // 10 // Code for using the result data ‘y’ and ‘t’. end;
The solution result for changing value of ‘b’ parameter presented on the picture below.
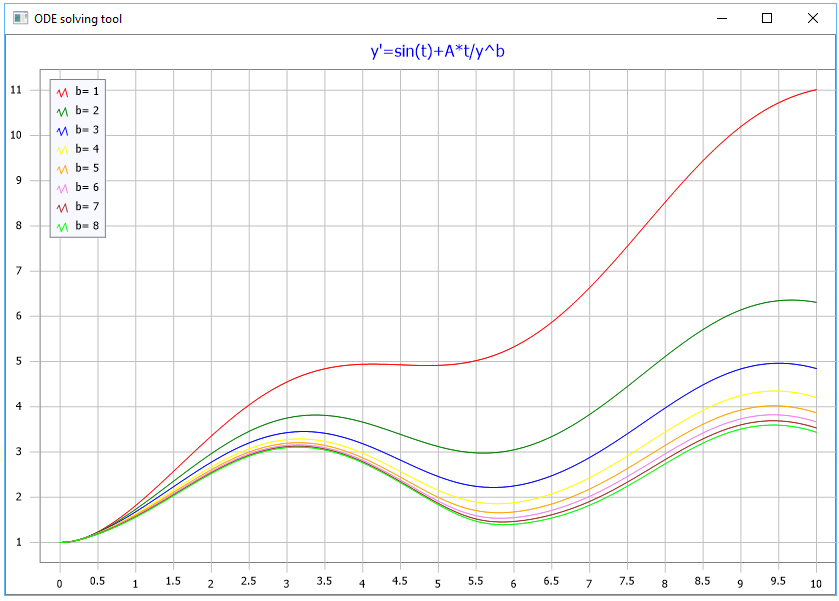
TMSFNCChart cross-platform / cross-framework chart displaying the result
As can be seen from the code above, there is no need creating new analytical ODE instance for exploring the parametric problem. As the analytical ODE is parametric, it is solved for the current parameter values and they can be easily changed via parametric interface.
Other advantages of using the numerical ODE tool with the symbolic calculus are:
- Minimal code writing, because there is no need to write special classes for the function method references (delegates) as in other numerical libraries.
- Convenient data representation for the developer and user as math expressions, not as programming code.
- Easily using the user input data (string data) for manipulations in programming code.
- Easily transfer input data via network as strings, easily storing and serializing the data.
The TMS Analytics and Physics pack includes the library with 5 ready-to-use numerical tools totally integrated with analytical features, such as symbolic derivatives. The trial version of TMS Analytics and Physics pack can be downloaded here. Total source code of the example application of ODE tool can be downloaded here.
Bruno Fierens
This blog post has not received any comments yet.
All Blog Posts | Next Post | Previous Post