Blog
All Blog Posts | Next Post | Previous Post
Array and Matrix operations with Analytics 2.2
Tuesday, September 26, 2017
New version 2.2 of TMS Analytics and Physics pack includes total support of operations with N-element arrays and MxN matrices. The operations realized in the Linear Algebra extension package. Array and matrix operations allow advanced calculations with small, compact formulae.Let us consider the examples of using the array/matrix operations for solving some common math/statistics problems. First of all we need to add special variables to the translator instance:
var
av: TArray<TFloat>;
mv: TArray<TArray<TFloat>>;
begin
translator:= TTranslator.Create;
translator.Add('µ', 0.0);
av:=TArray<TFloat>.Create(0.2, -0.1, -0.25, 0.4);
translator.Add('A', av);
av:=TArray<TFloat>.Create(-0.2, 0.2, -0.1, 0.25, 0.35, 0.15, -0.04, 0.01, -0.12, 0.1);
translator.Add('B', av);
SetLength(mv, 4, 3);
mv[0,0]:= 0.5; mv[0,1]:=-0.4; mv[0,2]:= 0.33;
mv[1,0]:=-0.3; mv[1,1]:= 0.1; mv[1,2]:= 0.28;
mv[2,0]:=-0.4; mv[2,1]:=-0.2; mv[2,2]:=-0.75;
mv[3,0]:=0.44; mv[3,1]:=0.25; mv[3,2]:= 1.00;
translator.Add('M', mv);
end;
The first problem to solve is calculation of statistics square deviation from the mean value for the ‘B’ array. Math formula for the deviation of discrete random variable is (https://en.wikipedia.org/wiki/Standard_deviation):
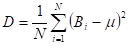where µ is the mean value 
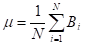N is the number of elements.
This formula can be evaluated with using array operations by the following code:
var
m, d: TValue;
begin
m:= translator.Calculate('∑B/#B');
translator.Variables['µ'].Value:= m;
d:= translator.Calculate('∑((B-µ)^2)/#B');
// print the ‘d’ value
end;µ = ∑B/#B = 0.06
D = ∑((B-µ)^2)/#B = 0.02876
Next problem is solving an over-determined linear equation system with the least squares approach (https://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)). Let the system is set up by the ‘M’ matrix and the ‘A’ vector. Then the solution ‘X’ is defined by the formula:
where MT – is the transposed matrix, 1 means the inversed matrix.This formula can be evaluated with the Analytics library as the following ‘M'*A/(M'*M)’. Here the apostrophe ‘'’ operator is for transposition operation and the division is equivalent to the multiplication by the inversed matrix. Evaluating the formula we get the following output:
X = M'*A/(M'*M) = TArray<TFloat>[3]=
(0.459953357586789 0.163947437790482 0.113927221302585 )
Here the ‘X’ array is the solution vector that minimizes the square error for the over-determined system.
As can be seen from the examples above, the realized array/matrix operations allow easily solve complicated problems with small, compact formulae. The complicated code for the array/matrix operations implemented inside the Analytics library and totally integrated with analytical evaluations. For an example, linear algebra operations allow solving so called ‘matrix’ ordinary differential equations (https://en.wikipedia.org/wiki/Matrix_differential_equation).
The TMS Analytics and Physics pack version 2.2 can be downloaded here.
Nancy Lescouhier
This blog post has received 1 comment.
All Blog Posts | Next Post | Previous Post
van der Linden Scott